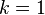Skip to end of metadata
Go to start of metadata

You are viewing an old version of this page. View the current version.

Compare with Current View Version History

« Previous Version 4 Current »

Conteúdo

Simulação

Nos serve para realizar Staffing, ou seja saber quantos agentes preciso no meu Contact Center para atender chamadas, Também é interessante para fazer ForeCastingestimando os volumes de crescimento do Contact Center saber quantos agentes vou precisar para chegar às métricas de Nível de serviço ou abandono desejadas.

Erlang

Em estatística, a Distribuição de Erlang é uma distribuição de probabilidade contínua com dois parâmetros, k e , cuja função de densidade para valores é:

A distribuição de Erlang é equivalente à distribuição gama com o parâmetro e . Para , isso é a distribuição exponencial. A distribuição de Erlang é utilizada para descrever o tempo de espera até o evento número k em um processo de Poisson.


Propriedades

  • Sua hipótese é dada por:

E(X) = k/λ

  • Sua variável é dada por:  

V(X) = k/λ²

  • A função geradora de momentos responde à expressão:

(1 - t/λ)⁻ᵏ

Erlang A

Extensão para Erlang C são adicionados abandonos nas filas. A espera do cliente é modelada como uma distribuição exponencial. 

Avaliar nível de serviço, probabilidade de espera, taxa de abandono e tempo médio de espera (Espera) de um sistema de filas. A diferença com C é que inclui abandonos. Cada cliente tem uma paciência com distribuição exponencial aleatória. É um sistema de filas estáveis por abandono.

A fórmula usada para o cálculo é a de aproximação, SLD baseada em equações de difusão, é usado do paper de Garnett, Mandelbaum e Reiman (2002), a cauda é infinita em capacidade.

Medidas de Performance

  • Nível de serviço (SL): A proporção de clientes que esperaram t ou menos para ser atendido. :

    • SL1: Clientes que abandonaram, mas esperaram como máximo t são excluídos do cálculo (usado no dashboard de filas/campanhas) SL1(y,t )=𝔼[X (y,t )] / 𝔼[A−G(y,t )]  

    • SL2: Clientes que abandonaram, mas esperaram no máximo t são contados como OK  SL2(y,t)=E[X(y,t)+G(y,t)] / E[A].

    • SLD: Aproximação baseada em equações de difusão. Fórmula do trabalho de Garnett, Mandelbaum e Reiman (2002).


    SL1 ≤ SL2. 

Para filas com alto tráfego usar SLD.

  • Probabilidade de espera: Probabilidade de um novo cliente entrar para esperar na fila.

  • Taxa de abandono: Proporção de clientes que cortaram sem ter resposta.

  • Espera: tempo médio de espera dos clientes (incluindo abandonos e atendidos).

Parámetros

  • Número de chamadas: A média do número de chamadas por medida de tempo. Exemplo: 5.7 clientes por minuto.

  • Tempo médio de conversação: Tempo médio de chamada. Exemplo: 2,5 minutos por cliente.

  • Tempo médio de espera: A média de tempo que um cliente está disposto a esperar. Exemplo: 2,3 minutos por cliente.

  • Nível de serviço esperado(Tempo de espera máximo desejado): É o valor do nível de serviço Exemplo: 20 segundos.

  • Tamanho da Fila: O tamanho máximo da cauda. Este número não pode ser muito maior do que a carga (quantidade de chamadas x nível médio de serviço) SLD conta infinito..

  • Tipo de nível de serviço: SL1, SL2, SLD.

  • Unidade tempo de espera: É a unidade para ser desdobrada do tempo de espera para saída de resultados.

  • Faixa de agentes: Permite avaliar medidas para múltiplos agentes. Exemplo: 5 e é avaliado para 10 agentes, então teremos dados de entre 5 a 15 agentes.

  • Avaliar quantidade de agentes: para um número específico de agentes.

  • Mínimo de agentes para nível de serviço %: Busca o mínimo de agentes necessários para obter um Nível de serviço (SL) maior ou igual ao target pedido. Y =min{y:SL(y,t )≥T ,y∈ℕ}

Exemplo: 80 e o tempo de espera aceitável para 20 segundos procurar a quantidade mínima de agentes necessários para ter pelo menos 80% de nível de serviço usando 20 segundos como máximo de espera do nível de serviço.

Exemplo:


Gráficas

1) Nível de serviço e probabilidade de espera

O gráfico mostra a probabilidade de um cliente entrar na fila de espera, bem como o comportamento do Nível de serviço para essas quantidades de agentes.

2) Taxa de Abandono

Porcentagem de clientes que cortaram sem ter uma resposta para essas quantidades de agentes.

3) Espera

O gráfico mostra a média de espera dos clientes, incluindo abandonos e atendidos. A unidade de tempo é selecionada antes da geração dos resultados.

Erlang B

Cálculo sem fila, avalia rejeição, não entra se todos os agentes estão ocupados. Nos dá a chance de não entrar um novo cliente se os agentes estiverem ocupados quando a chamada chegar.

Modelo clássico de filas M/M/c com modelo de entrada Poisson, tempo médio falado exponencial sem capacidade de colar (filas com máximo = quantidade de agentes). 

Probabilidade de abandono

É definida como a probabilidade de todos os agentes estarem ocupados quando um novo cliente tenta fazer contato.

Parâmetros

  1. Quantidade de Chamadas: A média de chamadas recebidas por unidade de tempo. Exemplo: 5,7 clientes por minuto.

  2. Tempo Médio de Atendimento: O tempo médio de duração das chamadas. Exemplo: 2,5 minutos por cliente.

  3. Intervalo de Agentes: Permite avaliar métricas para múltiplos agentes. Exemplo: Se o intervalo é de 5 e é avaliado para 10 agentes, então teremos dados entre 5 e 15 agentes.

  4. Avaliar Quantidade de Agentes: Com base na quantidade de agentes, calcula a probabilidade de abandono.

  5. Taxa Máxima de Abandono : Identifica a quantidade mínima de agentes necessária para garantir que a probabilidade de abandono seja igual ou inferior a um valor limite especificado. Supondo que B(y) seja a probabilidade de abandono em função do número de agentes y,  e  T o limite máximo permitido. representa o número mínimo de agentes necessários para que Y =min{y:B(y)≤T ,y∈ℕ}.. Exemplo: 5 agentes para garantir que a probabilidade de abandono não ultrapasse 5%.

Exemplo:

Gráficas

1) Probabilidade de Abandono:

Mostra a probabilidade de todos os agentes estarem ocupados quando um novo cliente tenta fazer contato.

 

Erlang C

Assume que os clientes têm paciência infinita ou seja, não há abandonos. Se houver abandono, então usamos Erlang A. Avalia nível de serviço, probabilidade de espera e tempo médio de espera (Espera) de um sistema de filas. Considerando o modelo clássico M/M/c, processo de Poisson, tempo de chamada exponencial e sem abandonos. Com capacidade de cauda infinita ou fixa. λ o número de chamadas 1/μ o tempo médio de espera, então a carga é ρ=λ/μ.

Medidas de Performance

  • Nível de serviço (SL): Número de clientes que esperaram igual ou menor do que o tempo médio de espera aceitável t                
    SL(y,t )=𝔼[X (y,t )]/𝔼[A]

  • Onde y é o número de agentes, X(y,t) é o número de clientes que esperam al menos t é uma função de y e t, A é o total de clientes, e  𝔼  o valor esperado estatístico.

  • Probabilidade de espera: Probabilidade de um novo cliente entrar para esperar na fila.

  • Tempo médio de espera dos clientes.

Parâmetros

  1. Quantidade de Chamadas: A média de chamadas por unidade de tempo. Exemplo: 5,7 clientes por minuto.

  2. Tempo Médio de Atendimento: Tempo médio de duração das chamadas. Exemplo: 2,5 minutos por cliente.

  3. Nível de Serviço Esperado (Tempo Máximo de Espera Desejado): O valor do nível de serviço. Exemplo: 20 segundos.

  4. Tamanho da Fila: Tamanho máximo da fila. Quando estiver cheia, os clientes não poderão entrar. -1 para infinito.

  5. Unidade para Exibir o Tempo Médio de Espera: Define a unidade para a apresentação dos resultados.

  6. Intervalo de Agentes: Permite avaliar métricas para múltiplos agentes. Exemplo: Se o intervalo é de 5 e é avaliado para 10 agentes, então teremos dados entre 5 e 15 agentes.

  7. Avaliar Quantidade de Agentes: Avaliação para um número específico de agentes.

  8. Número Mínimo de Agentes para o Nível de Serviço %: Identifica a quantidade mínima de agentes necessária para alcançar um nível de serviço (SL) igual ou superior ao objetivo. Exemplo: Se o objetivo é 80% de nível de serviço com um tempo máximo de espera de 20 segundos, o sistema busca a quantidade mínima de agentes necessária para garantir pelo menos 80% de SL com até 20 segundos de espera.

Exemplo:

Gráficas

  1. Nível de Serviço e Probabilidade de espera

O gráfico mostra a probabilidade de um cliente entrar na fila de espera, bem como o comportamento do Nível de serviço para essas quantidades de agentes.

  1. Espera

O gráfico mostra a média de espera dos clientes incluindo abandonos e atendidos para essas quantidades de agentes. A unidade de tempo é selecionada antes da geração dos resultados.

 

  • No labels